Analytic Analysis of Single and Three Phase Induction Motors

                                                Kent R. Davey
                                        American Electromechanics
                                           2275 Turnbull Bay Rd.
                                       New Smyrna Beach, FL 32168-5941

Abstract-The analysis of single and multiphase induction motors continues to represent a challenge to researchers in computational electromagnetics due to the presence of electric fields. This contribution cannot be inserted into the Green's function for boundary element codes; finite difference and finite element approaches are forced to hard code these effects, compensating at high speeds with upwinding techniques. The direct computation of these affects using transfer relations in a linear environment offers an analytical backdrop both for benchmark testing numerical codes and for design assessment criteria. In addition to torque-speed predictions, the terminal relations and total power dissipation in the rotor are computed
for an exposed winding three phase and single phase machine.

Introduction
    Rotational induced eddy currents involve a localized electric field. This term can be directly incorporated into finite element based analyses of induction motors as in [1],[ 2].Typically these types of approaches display non-physical oscillatory approaches with have been customarily handled using upwinding techniques [3],[ 4]. With boundary element codes, these velocity effects are ideally handled through a modification of the Green's function. Burnet-Fauchez [5],[ 6] was among the first to demonstrate the use of this modification for pure translation;unfortunately, these techniques do not work for rotational induced eddy currents.
    This paper is written for two purposes. First, it directly aids the designer in optimizing the performance of exposed winding machines. As superconducting field windings come closer to reality, such machines have certain advantages over conventional slot embedded windings [7]. If the iron is driven significantly into saturation, the need for the iron slots disappears. Because these slots are typically grounded, the voltage of the excitation windings can be significantly increased. However because the windings must sustain the magnetic forces, methods of support for the windings must necessarily be altered. Second and perhaps more importantly, the analysis results should serve as a benchmark problem for those working with numerical field codes suitable for such problems. The problem has been presented to the International TEAM workshop [8] to fill such a role.
    This paper combines techniques developed by Melcher [9] for analyzing induction motors and finite width/ depth windings. The techniques are applied to "real" windings rather than the surface windings focused on by Melcher in his induction device analyses.Additional attention is given to the prediction of torque in single phase devices using only power loss. This technique is especially suited to the boundary element and finite element codes that do not explicitly account for the rotational velocity

The Problem Defined
    Two induction motor problems are analyzed. The first, shown in Figure 1, is that of a three phase exposed winding motor. Each
 
 

Figure 1 Three Phase induction motor problem with a 45 degree winding spread per phase, holding J constant at 310 A/ cm 2 .

stator winding phase spans 45 . The current density is maintained constant at 310 A/ cm 2 with a frequency of 60 Hz. The object is to predict the torque, power dissipated, and stator terminal voltage induced for rotor angular velocities ranging from 0 to 1200 rad/ s, roughly three times faster than the stator field angular velocity of 377 rad/ s.

Figure 2 Single phase induction motor problem excited at 60 Hz.

    The second problem shown in Figure 2 is that of a single phase induction motor problem. The winding is excited at 60 Hz.The objective is to compute the torque-speed curve for a rotor angular velocity ranging from 0 to 358 rad/ s (0.95% of peak field speed). In addition, the terminal voltage and rotor dissipation are to be computed for both motors.

Fourier Decomposition of the Current
    Let NA represent the turns density for the phase A winding in Figure 1 with IA representing the current in the phase A winding. Using a similar nomenclature for the phase B and C windings, a Fourier spatial decomposition allows the current density for the three phase winding to be written

Assume that the three phases have the traditional time harmonic distribution with each phase having the same current density NI,
 

Component Strengths

Figure 3 Fourier component weighting for a three phase winding.

    Using Euler's rule to represent the cosinusoidal dependencies, (1) can be written

where H is the real part.
    In this form, it is clear that the three phase winding yields two counter-rotating waves. For this 3 phase winding, the components m= 3,9,15, etc. are equal to zero. With IN= 310 A/ cm 2and , the components are weighted as depicted in Figure 3.
The 5 th ,7 th ,11 th components have different slip frequencies than the fundamental. In a single phase machine, (3) takes the form

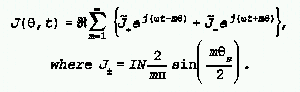
Transfer Relation Analysis
    The problem of Figure 1 consists of multiple piecewise homogeneous regions. The solution can now be developed in each region using the transfer relation concept fostered by James Melcher [10]. In non-conducting regions, the magnetic vector potential A is assumed to have a coulomb gauge dependence and satisfies the Poisson equation,

    Solutions take the form A = H{A( r, t) exp(-jm )} = H{ A~(r)exp[ j( t-m )]}. It is best to analyze the problem on a component by component basis for a fixed m. With J= 0, the vector potential satisfies Laplace's equation. Recall that . In terms of the vector potential's value on the outer surface A~alpha and that on the inner surface A~beta , the vector potential at any radius r is

    This forms the relation between the vector potential A and Ho,the transfer relation. From (6), the relations for the vector potential in the air gap, stator back iron, and outside the stator (r> r5 ) follow as

where

    In the winding region, r3 <r< r4 , A satisfies the Poisson equation, having both a homogeneous and a particular solution. Using complex notation, the mth component of the current density is

    If the current density has no radial dependence, Melcher has shown that the vector potential solution for any component m in the winding region takes the form

 

    The final region to be considered is the rotor in which eddy currents reside. The vector potential satisfies the Helmholtz equation,

or in cylindrical coordinates with a rotation angular velocity omega,

    Following the same nomenclature as (6), the solutions take the form on the outer and inner radii of any annulus of

    With this result, the vector potential for r< r2 is

where

and Jm and Hm are the Bessel and Hankel functions of the first kind, and Im and Km are the modified Bessel functions of order m.
    The field solution must satisfy the requirements that the tangential components of H(Ho ) and E(-j (w-mO)Am ) are continuous across a material interface. Combining (13) through (19) yields the matrix equation,

    Thus the vector potential and the tangential H field are computed on a component by component basis by inverting (24).

Post Processing for Output Quantities
    The average torque per unit depth is found by either integrating the Maxwell stress tensor r~xF~ force around the air gap or through a knowledge of the power dissipation in the rotor. Using the former approach just in the air gap outside r2 gives

    The electric field commensurate with the mth component of the vector potential Am in the z direction is Em=(-j (w-mO)Am ) The total power dissipation per unit depth in the rotor is

    By contrast the power dissipation just in the aluminum shell of the rotor is

    The final quantity of interest is the voltage induced in the phase A winding. In particular we seek the voltage induced per unit depth per turn. The winding is assumed to be comprised of n turns per unit cross-sectional area. The flux linking the phase A winding is

The integration can be carried out directly to give

The vector potential can be solved at any point in the winding as [11]

The particular solution Ap~ solves or in cylindrical coordinates

For m not equal to 2, Jm was defined as in (3) for the three phase machine or (4) for the single phase motor. The contribution from the + and -going waves must be superimposed. The voltage follows from the flux simply by multiplying by jW ; performing the radial integration in (30) yields

and hm is defined in (14). It is emphasized that the contribution from both the + and -going waves must be included in this summation.

Results
    Having an analytical expression allows design flexibility by way of optimization, which was one of the objectives of this document. The second objective was to realize a benchmark design for researchers to index numerical codes against. With that in mind, it is necessary that much of the data be presented in tabular format. The calculations were performed using as an upper limit for m of 50 for the three phase calculations and 100 for the single phase results. The primary quantities, torque, voltage, and power dissipation for the three phase motor are displayed in Table I. The fourth column represents the total rotor loss in both the aluminum and the rotor steel. All quantities are computed on a per unit depth (1 m) basis. The final column represents just the rotor steel loss due to I*I*R dissipation. The induced voltage in the phase A coil is computed as if the stator winding were comprised of a single turn.
    Table I Three phase predictions of torque, voltage, and power dissipation.

    Researchers who have attempted to work with single phase induction motors know of the difficulties of obtaining an accurate torque prediction; this torque results qualitatively from the subtraction of the effect of two counter-rotating traveling waves. Table II( shows the torque, voltage, and power dissipation for the single phase machine.

Table II( Torque, voltage, and power dissipation in the single phase motor of Figure 2.

Verification
    These results have been checked perfunctorily using a boundary element numerical analysis code. With the three phase motor, the problem can be analyzed at the slip frequency to derive these results. Figure 4 shows the comparison of analytical and computed torques and voltages. The last curve results from first numerically computing the power dissipation in the rotor at

    Figure 4 Three phase prediction of torque and voltage for the motor shown in Figure 1.

the slip frequency and then dividing by the slip frequency differential (difference between the synchronous speed and the mechanical rotation)[ 12]

    T=   W/(wo-wn)

Figure 5 Computed Torque for the single phase induction motor using rotor power loss.
    A similar confirmation was performed for the single phase machine. Numerically, this torque must be computed through the computation of the rotor power dissipation at both the + and -going wave speeds as

Conclusions
    A transfer relation technique has been outlined and applied to the study of exposed winding 3 phase and single phase induction motors. The results may form analytical backdrop for optimization studies. In addition they serve as a benchmark for indexing the performance of numerical codes for these types of problems.

References
1. R. Belmans, R. D. Findlay, and W. Geysen, "A circuit approach to finite element analysis of a double squirrel cage induction
motor", IEEE PES Summer Meeting, Minneapolis, Minnesota, July 15-19, 1990.

2. C. Rajanathan and B. Watson, "Simulation of a Single Phase Induction Motor Operating in the Motoring, Generating, and
Braking Modes", IEEE Trans. Magn., vol. 32, no. 3, May 1996, pp 1541-1544.

3. J. C. Heinrich, P. S. Huyakorn, O. C. Zienkiewicz, "An Upwind Finite Element Scheme for Two-Dimensional Convective Transport
Equation", Int. J. Num. Meth. Eneng., Vol. 11, pp 131-144, 1977.
4. H. T. Yu, K. R. Shao, K. D. Zhou, "Upwind-Linear Edge Elements for 3D Moving Conductor Eddy Current Problems", IEEE Trans. MAG-32.,
No. 3, May 1996, pp. 760-763.
5. M. Burnet-Fauchez and R. Michaux, "Boundary Element Calculation of 2D magnetic fields with eddy currents", Modelec
Conf. La Grande Motte, Oct. 1984, Pluralis Ed. Paris, pp 97-109.

6. M. Burnet-Fauchez, "Calculation of eddy currents in moving conductors using boundary element methods", Proc. COMPUMAG,
Colorado State, Fort Collins, June 3-6, 1985.
7. J. L. Kirkley, "Design and Construction of an Armature for an Alternator with a Superconducting Field Winding", Ph. D. Thesis,
Department of Electrical Engineering, Massachusetts Institute of Technology, Cambridge, Mass., 1971.

8. L. Turner, K. Davey, C. Emson, K. Miya, T. Nakata, and A. Nicolas, "Problems and Workshops for Eddy Current Code
Comparison", IEEE Transactions on Magnetics, vol. 24, no. 1, pp. 431-434, January 1988.

9. J. Melcher, Continuum Electromechanics, MIT Press, Cambridge, MA, 1981, Section 4.9, 6.5.
10. James Melcher, Continuum Electromechanics, MIT Press, Cambridge Press, 1981, p. 2.45, and 6.13-6.14.
11. J. R. Melcher, op. cit., pp. 4.27-4.28.
12. Kent Davey, "Rotating Field Analysis Using Boundary Element Methods", submitted to IEEE Trans. Magnetics, Compumag-Rio, 19 97.